Kanasan.JS JavaScript第5版読書会でベジエ曲線について発表した

JavaScript 勉強会

2011年01月15日(土) に京都で Kanasan.JS JavaScript第5版読書会 #11 が開かれた(告知ページ)。みんなでサイ本を読む会だ。第1回からだいたい3年ぐらい続いてて、今回でいよいよ最終回となった。僕は途中半分の第6回くらいからの参加なんだけど、最後のまとめとして気合いを入れて参加した。

読んだところ

今回は P561 から P629(最後)まで。主にクライアントサイドのグラフィック制御のところを読んだ。

いろんなグラフィック関係のテクニックが書いてあったけど、本が出てから時間がたってることもあって今では使わないようなものもあった。その中で注目はやっぱり SVG と canvas 要素。サンプルコードが書いてあったのでみんなで読んだ。

SVG

SVG は XML で定義された画像フォーマットの一種。V は Vector の V で、その名の通りベクターグラフィックになってる。HTML の中に SVG を埋め込めて、さらにそいつを JavaScript から操作できる。

指定した経路に沿って線を書くこともできる。例えば扇形を書くときはこんな風に経路を指定する。

// この文字列に線の経路情報を保持する
var d = "M " + cx + "," + cy +    // 始点(円の中心)
        " L " + x1 + "," + y1 +   // 始点から (x1, y1)まで直線を引く
        " A " + r + "," + r +     // 円弧の半径
        " O " + big + " 1 " +     // 円弧の向き。
                                  // 終端まで弧を書く際に近いほう/遠いほうのどちらを通るかを指定する
        x2 + "," + y2 +           // 円弧の終端
        " Z";                     // 始点まで戻って終わり

超読みにくい。でもこんな指定を繰り返すと円グラフが描けたりする。

canvas 要素

canvas 要素は JavaScript で動的に画像を描くための要素。できあがりはビットマップ画像になる。lineTo, arc などの API を使ってチマチマ画像を描いていく。その後僕は発表したんだけど、そこでも canvas を使った。

ベジエ曲線について

今回はグラフィック関連の章ということで、僕はベジエ曲線について発表した。

ベジエ曲線って名前は聞いたことある、もしくは使ったことあるっていう人も多いんじゃないのかな。 Illustrator, Photoshop とかでも描けるし、canvas 要素の quadraticCurveTo(2次)、bezierCurveTo(3次)という API でも描ける。

でもアルゴリズムまでは知ってる人少ないと思う。僕は学校でそういうの勉強したので、いい機会だと思って発表した。

ベジエ曲線とは

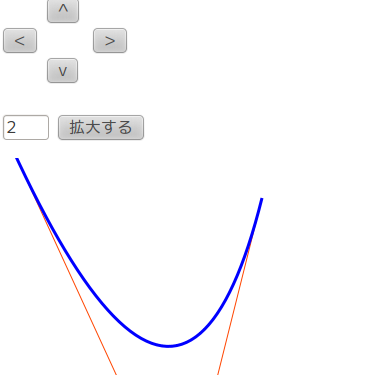
ベジエ曲線とは、線分の内分点を取る操作を繰り返すことにより得られる曲線のこと。といってもよく意味が分からないかもしれない。jsdo.it でデモページを作ったので適当に遊んで欲しい。

入力となるいくつかの点があって、そこからアルゴリズムに基づいて曲線を描く。その「いくつかの点」というのを制御点という。Illustrator では「開始地点のアンカーポイント」とか呼ばれてるやつね。

数学的な理論の話は「ベジエ曲線とベジエ曲面」というページに書いてある。大学の講義用の資料でかなり本格的。その中で、曲線の定義、表現方法は「ベジエ曲線とベジエ曲面１」と「ベジエ曲線とベジエ曲面２」を読むと分かる(どっちも PDF ファイル)。

JavaScript での実装

僕のデモページで一番大事な関数は以下。ベジエ曲線上の1点を求めてる。

// bezierCurve.js 58行目

// 与えられた制御点に対して、 t を固定して得られる
// ベジエ曲線上の1つの点を取得する
// @points : 任意の数の制御点を格納した配列
bezierPointT : function(t, points) {
    if (points.length >= 2) {
        var dividedPoints = [];
        for (var i = 0; i < points.length - 1; i++) {
            dividedPoints.push(
                BezierCurve.dividePoint(t, points[i], points[i+1]));
        }
        return BezierCurve.bezierPointT(t, dividedPoints);
    } else {
        return points[0];
    }
}

この t を0から1まで動かせばなめらかな曲線になる。実際には連続的に無限の点を求めることはできないので、0から1までを適当に分割して折れ線で近似してる。

拡大/縮小、平行移動

ベジエ曲線の便利な性質として「アフィン写像に対して普遍」というのがある。なんかまた難しい用語が出てきたけど、かみ砕いて言うと以下の通り。

  • ベジエ曲線を描いてから曲線全体を平行移動させるのと、先に制御点を平行移動してからベジエ曲線を描くのとでできる結果は同じ
  • 回転、拡大、縮小、鏡写しについても同様
  • そういう変換の組み合わせでも同様

この性質については、さっきの講義ページでは「ベジエ曲線とベジエ曲面６」に解説がある(これも PDF)。

実際に曲線を変換する場合は後者の方法、先に制御点を変換する方が楽に実装できる。

さらに、拡大の場合なんかは曲線全体を拡大すると困ることがある。曲線とは言っても実際には折れ線で近似していることを思い出そう。小さいうちは折れ線には見えなくても、拡大すると角の部分も拡大されるのでカクカクに見えてしまう。

そんな場合でも、後者の方法の場合は拡大した分だけ分割数を増やせば角は見えなくなる。曲線のアルゴリズムだけ決まっていて実際の精度は描画する時に決めれるので、必要に応じて精度を上げるということができるのだ。これが「ベクター画像は拡大してもギザギザがでてこない」という理由になってる。ベジエ曲線便利。

実用上はこういう理論を知らなくても必要なところだけ利用すればいいんだけど、数学を使うと「その性質が必ず成り立つ。絶対に大丈夫」という保証ができる。数学って何してるのかいまいち分かりにくいところがあるけど、こんなところに役に立ってる例があった。

あと、最初に言ったように canvas にはベジエ曲線を描く API があるので、これに実用上の意味はない。アルゴリズムを理解するためのサンプル。

そんなこんなで読書会は無事最後まで終了した。

最後に

思い出してみると、僕が初めて参加した勉強会が Kanasan.JS だった。それから2年以上たって、僕のプログラミングのレベルも上がったし、いろいろ発表するようにもなった。この勉強会を通して学んだことは大きかった。

Kanasan.JS はいろんな勉強会の中でもトップクラスの技術レベルだと思う。それもみんなで本を読んだりして勉強した結果だ。メンバーが入れ替わりながら何年も継続できているのは、この勉強会を大切に感じている人がいるからこそだと思う。そして、そういう流れを作ってくれた初代代表の Kanasan にはとても感謝しています。

今回でサイ本読書会が終わったので、次回以降は jQuery コードリーディングと単発企画ものを行う。これからも継続して、関西を代表する勉強会になればいいと思う。